1. Phân loại hiệu quả kinh doanh ngân hàng
Hiệu quả kinh doanh ngân hàng theo cách tiếp cận đường biên hiệu quả là cách tiếp cận hiện đại với việc hiệu quả kinh doanh của ngân hàng sẽ được đánh giá bằng mối quan hệ giữa đầu vào mà ngân hàng sử dụng và sản phẩm đầu ra mà ngân hàng đó tạo ra. Trong các nghiên cứu về hiệu quả kinh doanh theo phương pháp này, đáng chú ý là nghiên cứu của Farrel (1957) vì đã lần đầu tiên làm rõ khái niệm hiệu quả kinh doanh cũng như cách nhận dạng của từng loại hiệu quả kinh doanh, cũng như việc mô hình hóa chúng. Farrel (1957) giới thiệu về đường biên hiệu quả trong đó một tổ chức có thể tối đa hóa đầu ra dựa vào một lượng đầu vào nhất định. Từ đó, hiệu quả kinh doanh của một tổ chức bao gồm hiệu quả kỹ thuật, hiệu quả phân bổ và hiệu quả kinh tế.
Khái niệm về hiệu quả kỹ thuật thật ra đã được giới thiệu trước đó bởi Koopmans (1951) khi ông cho rằng một tổ chức được coi là có hiệu quả về kỹ thuật nếu như tổ chức đó không thể tăng một đơn vị đầu ra mà không cần giảm ít nhất một đơn vị đầu ra khác hoặc tăng ít nhất một đơn vị đầu vào. Hiệu quả kỹ thuật cũng được thể hiện ở việc một tổ chức không thể giảm một đơn vị đầu vào này mà không cần tăng một đơn vị đầu vào khác hay giảm ít nhất một đơn vị đầu ra.
Hiệu quả kỹ thuật còn được hiểu là khả năng tối đa hóa đầu ra từ một số lượng đầu vào nhất định hay tối thiểu hóa đầu vào để thu được một lượng đầu ra nhất định. Một tổ chức được coi là không hiệu quả về mặt kỹ thuật nếu như tổ chức đó không thể tạo ra được đầu ra lớn nhất từ một lượng đầu vào cố định. Nói một cách khác, tổ chức đó đang hoạt động tại điểm nằm ngoài đường biên hiệu quả.
Hiệu quả phân bổ là khả năng kết hợp tối ưu các yếu tố đầu vào với một công nghệ cho trước cũng như với một mức giá cả đầu vào xác định. Một tổ chức được coi là phi hiệu quả về mặt phân bổ nếu như tổ chức đó không thể sử dụng một cách tiết kiệm đầu vào, hay là không tìm được các đầu vào thay thế có mức giá rẻ hơn để sản xuất một lượng đầu ra tương tự.
Theo Farrel (1957), hiệu quả kỹ thuật và hiệu quả phân bổ cấu thành hiệu quả kinh tế của tổ chức đó. Hiệu quả kinh tế được đo lường bằng tích số giữa hiệu quả phân bổ và hiệu quả kỹ thuật và nhận giá trị trong khoảng (0,1).
Các nghiên cứu về hiệu quả kinh doanh ngân hàng cũng sử dụng các khái niệm về hiệu quả kỹ thuật, hiệu quả phân bổ và hiệu quả kinh tế giống như Farrel (1957) đã đề xuất. Bên cạnh đó, khái niệm về hiệu quả kinh doanh mở rộng hơn với hiệu quả quy mô (Fare, Grosskopf và Lowell, 1985), hiệu quả chi phí (Berger và Mester, 1997) hay hiệu quả lợi nhuận (Berger và Mester, 1997).
2. Các cách tiếp cận trong xây dựng đường biên hiệu quả
2.1. Cách tiếp cận hướng về đầu vào
Với cách tiếp cận đầu vào, hiệu quả kinh doanh và ý tưởng về đường biên hiệu quả được Farrell mô tả cụ thể trong hình 1.1. Trong tình huống này, Farrell (1957) giả sử một ngân hàng sử dụng hai đầu vào (x1 và x2) để tạo ra một đầu ra duy nhất là (y) trong điều kiện công nghệ sử dụng tại ngân hàng là không đổi. Giả định ngân hàng đó có thể kết hợp các đầu vào để tạo ra một lượng đầu ra q nhất định mô tả bằng đường biên SS’, đường SS’ là đường đồng lượng. Đường thẳng AA’ mô tả cách kết hợp các đầu vào tương ứng với một mức tổng chi phí đầu vào nhất định, vì vậy, đường AA’ gọi là đường đồng phí. Điểm Q’ là điểm tiếp xúc giữa đường cong SS’ và đường AA’ là điểm hiệu quả cả về kỹ thuật và phân bổ. Nếu tổ chức đó tiến hành sử dụng đầu vào trong sản xuất được mô tả ở điểm P thì tổ chức đó không hiệu quả cả về kỹ thuật và phân bổ. Mức độ không hiệu quả về kỹ thuật thể hiện bằng tỷ lệ OQ/OP. Khoảng cách PQ cho biết tổ chức đó hoàn toàn có thể giảm được lượng đầu vào theo một tỷ lệ nào đó trong khi số lượng đầu ra không đổi.
Hiệu quả phân bổ được đo bằng tỷ lệ OR/OQ, tỷ lệ này cho biết khả năng tiết kiệm chi phí mà tổ chức còn có thể thực hiện được để tạo ra lượng đầu ra không đổi Từ đó mức độ hiệu quả kinh tế (EE) của tổ chức hoạt động tại điểm P là sự kết hợp giữa hiệu quả kỹ thuật và hiệu quả phân bổ được xác định bằng các công thức:
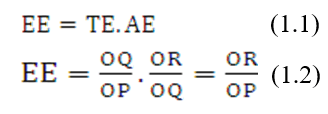
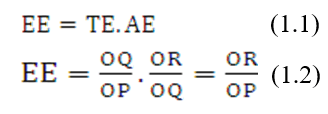
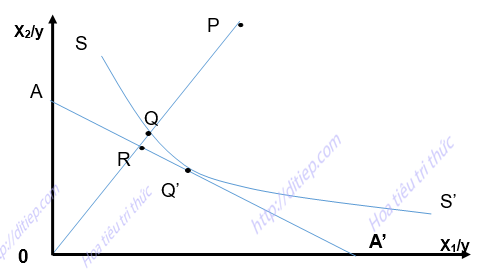

Hình 1.1. Hiệu quả kỹ thuật và hiệu quả phân bổ theo cách tiếp cận hướng về đầu vào. Nguồn: Farrell (1957)
Theo hình 1.1, tổ chức hoạt động tại điểm Q được coi là có hiệu quả về kỹ thuật nhưng không có hiệu quả phân bổ. Tổ chức hoạt động tại điểm R có hiệu quả về mặt phân bổ nhưng không có hiệu quả về mặt kỹ thuật.
Từ công thức 1.1 có thể thấy, tỷ lệ EE luôn nằm trong khoảng (0,1) trong đó nếu tổ chức nào có tỷ lệ này nhận giá trị cao nhất bằng 1 nghĩa là tổ chức đó có hiệu quả về mặt kinh tế (kỹ thuật và phân bổ) theo quan điểm của Farrel (1957).
Trong thực tế, có thể không thể ước lượng được đường đồng lượng SS’ như thể hiện trong hình 1.1, đường đồng lượng có thể được ước lượng từ một số liệu mẫu (Coelli, 2008). Lúc này, đường cong SS’ trở thành đường đồng lượng lồi tuyến tính từng khúc phi tham số như trong hình 1.2 dưới đây.
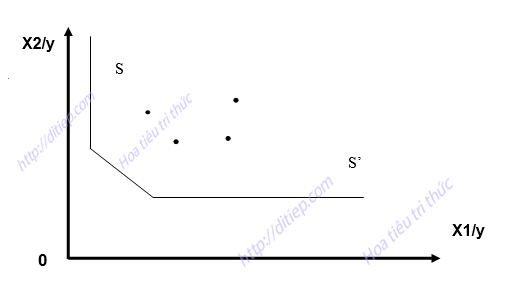

Hình 1.2. Đường đồng lượng tuyến tính từng khúc. Nguồn: Coelli (1996)
2.2. Cách tiếp cận hướng về đầu ra
Trong cách tiếp cận hướng về đầu vào, hiệu quả kinh doanh được đánh giá bằng cách trả lời câu hỏi ngân hàng có thể tiết kiệm chi phí được nữa hay không và bằng bao nhiêu nếu như lượng đầu ra tạo được vẫn không thay đổi. Ngược lại, trong cách tiếp cận hướng về đầu ra, hiệu quả kinh doanh ngân hàng liên quan đến khả năng ngân hàng có thể tăng được lượng đầu ra hay không nếu như lượng đầu vào sử dụng là không đổi. Lý giải về cách tiếp cận này trong đánh giá hiệu quả kinh doanh ngân hàng được mô tả trong hình 1.3.
Trong hình 1.3, sự phi hiệu quả kỹ thuật được thể hiện bằng khoảng cách AB, được hiểu là lượng đầu ra mà ngân hàng có thể gia tăng mà không cần phải bỏ thêm các chi phí đầu vào. Vì thế hiệu quả kỹ thuật theo cách tiếp cận này được tính bằng công thức:
![]()
![]()
Nếu như cho biết các thông tin về giá các đầu vào thì đường đẳng thu DD’ được xác định và khi đó, hiệu quả phân bổ được xác định là lượng đầu ra có thể gia tăng khi chi phí đầu vào không đổi. Hiệu quả phân bổ được xác định dựa trên công thức:
![]()
![]()
Từ đó, hiệu quả kinh tế được xây dựng bằng công thức:
![]()
![]()
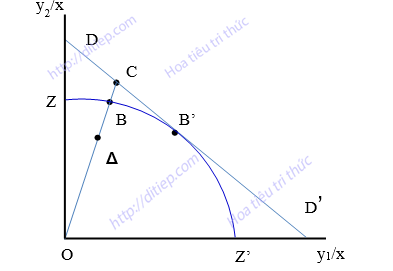

Hình 1.3. Hiệu quả kinh doanh hướng về đầu ra. Nguồn: Farrell (1957)
3. Khái quát các cách tiếp cận về hoạt động kinh doanh ngân hàng
Việc xác định các biến đầu vào và đầu ra để xây dựng đường biên hiệu quả phụ thuộc vào cách tiếp cận hoạt động kinh doanh ngân hàng. Vì ngân hàng là một chủ thể kinh doanh tương đối đặc biệt, nên tồn tại một số cách tiếp cận khác nhau như cách tiếp cận “sản xuất”, cách tiếp cận “trung gian tài chính”, cách tiếp cận “hướng về lợi nhuận” và cách tiếp cận “giá trị tăng thêm”. Liên quan đến các cách tiếp cận này, Fadzlan Sufian (2011) cho rằng kết quả đánh giá hiệu quả kinh doanh ngân hàng phụ thuộc rất nhiều vào việc lựa chọn các biến mô tả hoạt động ngân hàng.
Cách tiếp cận “sản xuất” đưa ra bởi Benston (1965) được coi là cách tiếp cận truyền thống khi ngân hàng được coi là một chủ thể tạo ra các dịch vụ cho người gửi tiền hay nói cách khác hoạt động của ngân hàng nhằm biến đổi các khoản tiền gửi thành các khoản cho vay. Theo quan điểm này, đầu vào của quá trình sản xuất đó là nhân viên ngân hàng và các tài sản hữu hình trong khi đầu ra là các tài khoản cho vay. Tuy nhiên, cách tiếp cận này dường như bỏ qua một hoạt động quan trọng của ngân hàng là hoạt động đầu tư (Berger and Humphrey, 1997).
Ngược lại, cách tiếp cận “trung gian” lại cho rằng ngân hàng đóng vai trò là một trung gian giữa người cho vay và đi vay. Chính vì vậy, đầu ra của hoạt động ngân hàng chính là tổng số tiền cho vay và các khoản đầu tư chứng khoán trong khi đầu vào của quá trình đó là các khoản tiền gửi, nguồn nhân lực và các khoản tài sản hữu hình (Sealey, Calvin W, and James T Lindley, 1977). Cách tiếp cận trung gian tài chính còn được phát triển thành cách tiếp cận “giá trị gia tăng”, trong đó, các tài khoản như tiền gửi và cho vay đều được coi là đầu ra vì các khoản mục này có ý nghĩa tạo ra giá trị tăng thêm.
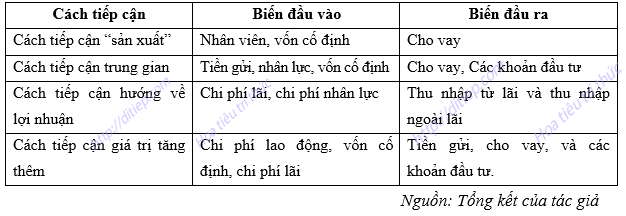
Cách tiếp cận “hướng về lợi nhuận” thì cho rằng ngân hàng cũng như một thực thể kinh doanh với mục tiêu cuối cùng là tạo ra thu nhập từ các khoản chi phí đã bỏ ra cho hoạt động kinh doanh đó (Drake và cộng sự (2006)). Vì vậy, đầu ra của hoạt động ngân hàng chính là tổng thu nhập (thu nhập từ lãi và ngoài lãi) và đầu vào là tổng chi phí (chi phí lãi và chi phí ngoài lãi). Tổng hợp cách phân loại các biến đầu vào và đầu ra được thể hiện trong bảng 1.3 dưới đây.
Bảng 1.3. Các biến đầu vào và đầu ra theo các cách tiếp cận về hoạt động ngân hàng

4. Đo lường hiệu quả kinh doanh ngân hàng
Hiệu quả kinh doanh ngân hàng được đo lường bằng hai phương pháp phương pháp tham số và phương pháp phi tham số. Cả hai phương pháp này đều sử dụng các vectơ đầu vào và đầu ra trong xác định đường biên hiệu quả. Sự khác nhau cơ bản của hai phương pháp này là ở chỗ phương pháp phi tham số không đòi hỏi một phương trình cụ thể cho việc xây dựng đường biên hiệu quả, trong khi đó, phương pháp tham số lại yêu cầu phải xác định một hàm số cụ thể cho các đầu vào và đầu ra đối với đường biên hiệu quả. Trong đó, đường biên được hiểu là giới hạn có thể đạt được, nghĩa là giá trị tối ưu trong một hoạt động kinh tế nào đó của một tổ chức. Chính vì thế, tổ chức nào đó hoạt động trên đường biên thì tổ chức đó được coi là hiệu quả nhất so với các tổ chức khác trong một ngành nào đó.
4.1. Phương pháp phi tham số
a) Giới thiệu về phương pháp phi tham số
Phương pháp phi tham số là phương pháp không đòi hỏi xác định một hàm số cụ thể mô tả mối quan hệ giữa đầu ra và đầu vào trong việc xây dựng đường biên hiệu quả. Ý tưởng về cách tiếp cận phi tham số lần đầu tiên được xuất hiện trong nghiên cứu của Farrell (1957) tuy nhiên trong suốt hai thập kỷ, cách tiếp cận này chưa thu hút nhiều sự quan tâm từ các học giả cho đến khi nghiên cứu của Charnes và cộng sự (1978) được công bố.
Charnes và cộng sự (1978) đã đề xuất một chương trình thuật toán, có tên gọi phân tích đường bao dữ liệu (Data envelopment analysis – DEA) để đánh giá năng lực của một số tổ chức có nhiều điểm đồng nhất với nhau trong việc sử dụng đầu vào để tạo ra một số đầu ra nhất định. Đường bao dữ liệu đóng vai trò như một đường biên hiệu quả để từ đó hiệu quả của từng tổ chức trong mẫu nghiên cứu được tính toán. Kể từ nghiên cứu đầu tiên đó, rất nhiều nghiên cứu sau này đã phát triển và hoàn thiện phương pháp đánh giá hiệu quả kinh doanh của ngân hàng dựa vào đường bao dữ liệu để khẳng định vai trò của phương pháp này trong đánh giá hiệu quả kinh doanh.
Phương pháp đường bao dữ liệu (DEA) sử dụng một chương trình tuyến tính để xây dựng một đường biên hiệu quả cho các đơn vị trong mẫu nghiên cứu từ các kết hợp đầu vào và đầu ra của các đơn vị đó. Mỗi đơn vị trong mẫu hay mỗi ngân hàng được gọi là một đơn vị tạo quyết định (Decision Making Units – DMUs). Từ đó, hiệu quả của mỗi DMU sẽ được tính toán bằng một điểm số căn cứ vào khoảng cách giữa đường biên hiệu quả này với thực tế hoạt động của ngân hàng. Điểm hiệu quả của mỗi ngân hàng nằm trong khoảng (0,1), ngân hàng có điểm hiệu quả bằng 1 là ngân hàng hoạt động trên đường biên hiệu quả và cũng là ngân hàng kinh doanh hiệu quả nhất trong mẫu.
Liên quan đến cách tiếp cận đường bao dữ liệu, Charnes và cộng sự (1978) giới thiệu mô hình CCR với giả thiết là hiệu quả không đổi theo quy mô. Sau đó, Banker, Charnes và Cooper (1984) lại giới thiệu một mô hình DEA mới tên là mô hình BCC với giả thiết là lợi nhuận thay đổi theo quy mô (VRS).
Hiệu quả kỹ thuật được tách thành hiệu quả kỹ thuật thuần và hiệu quả quy mô (Fare, Grosskopf và Lowell, 1985). Nói cách khác, sự phi hiệu quả về kỹ thuật xuất phát từ hai nguồn: sự phi hiệu quả về quy mô (SE) do các yếu tố phản ánh quy mô hoạt động của ngân hàng và sự phi hiệu quả kỹ thuật thuần túy (PTE), chẳng hạn trình độ quản lý ngân hàng. Liên quan đến hiệu quả quy mô, có hai trường hợp có thể xảy ra: hiệu quả không đổi theo quy mô (CRS) và hiệu quả biến đổi theo quy mô (VRS).
Việc tính toán hiệu quả quy mô được thực hiện theo một số bước như sau. Trước hết, hiệu quả kỹ thuật được xác định từ hai mô hình: mô hình hiệu quả không đổi theo quy mô (CRS) để có được hiệu quả kỹ thuật không đổi theo quy mô TECRS, mô hình hiệu quả biến đổi theo quy mô (VRS) để có được hiệu quả kỹ thuật thay đổi theo quy mô TEVRS. Nếu tồn tại sự chênh lệch giữa hai loại hiệu quả này nghĩa là có sự phi hiệu quả về quy mô. Hiệu quả quy mô, từ đó, được tính toán theo công thức:
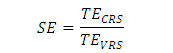
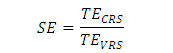
Hai mô hình CCR gắn với hiệu quả không đổi theo quy mô CRS và mô hình mô hình BCC gắn với hiệu quả thay đổi theo quy mô VRS được trình bày cụ thể dưới đây.
b) Mô hình CCR
Mô hình hiệu quả không đổi theo quy mô (CRS) gắn với giả thiết các ngân hàng đang hoạt động ở quy mô tối ưu. Mô hình CCR tính toán điểm hiệu quả của mỗi DMU bằng cách tính toán tỷ lệ giữa đầu ra và đầu vào có tính toán đến trọng số. DMU nào có tỷ lệ này lớn nhất thì được coi là có hiệu quả và bằng 1. Chính vì thế, điểm hiệu quả của các DMU còn lại sẽ nhỏ hơn hoặc bằng 1.
Giả sử trong mẫu nghiên cứu có n DMU và mỗi DMU sử dụng K đầu vào khác nhau với các lượng khác nhau và tạo ra M đầu ra khác nhau. Chẳng hạn, DMUj sử dụng vector xij đầu với m chiều vào và tạo ra yrj đầu ra với s chiều, mô hình hiệu quả không đổi theo quy mô CRS được xác định như sau:


Đường biên hiệu quả được xác định từ tập hợp điểm hiệu quả tối đa của các DMU nên vấn đề đặt ra là phải xác định các trọng số ur và vi là bao nhiêu để tối đa hóa hiệu quả của các DMU. Chính vì vậy, bài toán tối ưu trên phải được giải quyết để tìm ra bộ trọng số đó cho từng DMU. Tuy nhiên, nếu bộ trọng số (u*, v*) được xác định là nghiệm của bài toán thì tổng số nghiệm của bài toán này có thể là vô hạn vì bất kỳ một bộ trọng số (au*, av* với mọi a>0) cũng có thể là nghiệm của bài toán. Chính vì vậy, Charnes và Cooper (1962) cho rằng, một điều kiện về bộ trọng số (u,v) phải được đặt ra để chuyển bài toán trên thành một mô hình tuyến tính.
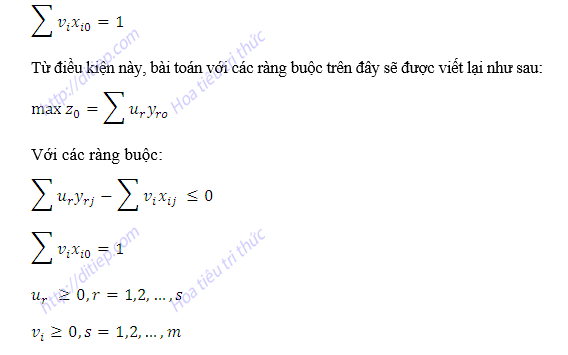
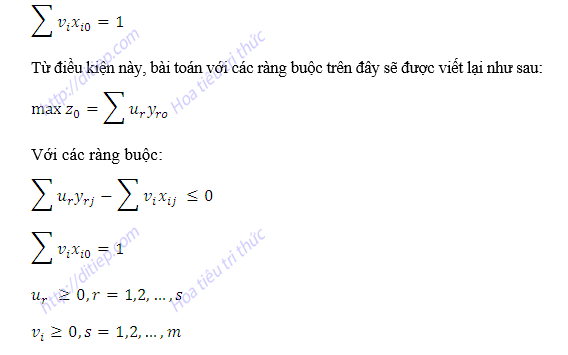
Từ mô hình cơ bản trên đây, hai mô hình tương ứng với hiệu quả từ việc tối thiểu hóa đầu vào và tối đa hóa đầu ra được xây dựng. Đối với mô hình hiệu quả đầu vào tức là hiệu quả đạt được do việc tối thiểu hóa đầu vào cho việc tạo ra một lượng đầu ra nhất định, gọi θ là chỉ số hiệu quả hay là điểm hiệu quả của DMU thứ i và λ vector trọng số. Khi đó, điểm hiệu quả sẽ có giá trị từ 0 đến 1, điểm hiệu quả bằng 1 chỉ DMU nằm trên đường biên hiệu quả, xác định trong mô hình:
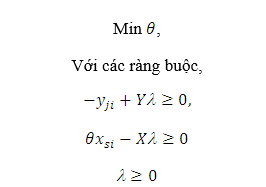
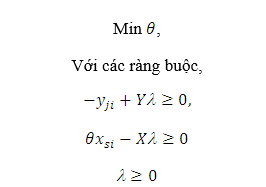
Tương tự đối với hiệu quả đầu ra được hiểu là hiệu quả có được do tối đa hóa đầu ra mà không cần phải sử dụng thêm bất kỳ đơn vị đầu vào, điểm hiệu quả của mỗi DMU được ký hiệu bằng η, μ là vector trọng số tương ứng với mô hình dưới đây.
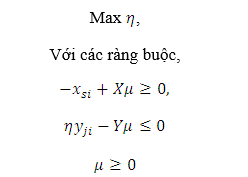
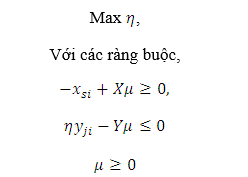
Từ khái niệm về hiệu quả kỹ thuật, có thể thấy hai mô hình trên đây đều dùng để đo lường hiệu quả kỹ thuật của các DMU. Do các trọng số λ và μ đều nhận giá trị dương, các ràng buộc trên cho biết các DMU này hiệu quả không đổi theo quy mô. Các điểm hiệu quả θ và η đều nhận giá trị trong khoảng (0,1), với ý nghĩa DMU có điểm nhỏ hơn 1 sẽ phi hiệu quả về kỹ thuật, còn DMU nào có điểm hiệu quả bằng 1 sẽ nằm trên đường biên hiệu quả.
c) Mô hình BCC
Mô hình CCR đưa ra bởi Charnes, Cooper và Rhodes (1978) được thiết lập dựa trên giả thiết là hiệu quả không đổi theo quy mô. Tuy nhiên, giả thiết này chỉ phù hợp khi các ngân hàng đang hoạt động ở quy mô tối ưu mà điều này khó xảy ra trong thực tế vì ngân hàng có thể gặp phải một số trở ngại trong môi trường kinh doanh của mình như quy định của Nhà nước hay sự không hoàn hảo của thị trường. Vì thế, mô hình CCR trở nên không hoàn toàn phù hợp để đánh giá hiệu quả của các tổ chức hoạt động trong các môi trường khác nhau. Chính vì vậy, sau này Banker, Charnes and Cooper (1984) đã bỏ giả thiết hiệu quả không đổi theo quy mô, và đề xuất một mô hình đánh giá hiệu quả của các DMU với giả thiết hiệu quả thay đổi theo quy mô. Mô hình này được đặt theo tên viết tắt của các nhà nghiên cứu và có tên là mô hình VRS.
Mô hình BBC được xây dựng dựa trên nguyên tắc của mô hình CCR nhưng kèm theo ràng buộc ∑λ = 1 (đối với hiệu quả từ tối thiểu hóa đầu vào) và ∑μ = 1 (đối với hiệu quả từ tối đa hóa đầu ra) để bảo đảm khi tính toán hiệu quả, các DMU cùng quy mô sẽ được so sánh với nhau. Từ đó, mô hình CCR có thể được viết lại như sau:

Phương pháp phi tham số (Phương pháp phân tích đường bao dữ liệu DEA) tìm ra ngân hàng nào có tỷ lệ đầu ra trên đầu vào tốt nhất, nghĩa là ngân hàng tạo ra được một lượng đầu ra nhất định với chi phí bỏ ra là thấp nhất trong mẫu nghiên cứu. Giả sử các đầu vào của các ngân hàng trong mẫu đều có cùng mức giá đầu vào thì hiệu quả của các ngân hàng còn lại trong mẫu được đo bằng cách so sánh chi phí của ngân hàng đó với ngân hàng tốt nhất trong việc cùng tạo ra một đầu ra nhất định. Ưu điểm của phương pháp này xuất phát từ việc phương pháp phi tham số không đòi hỏi phải xác định một hàm số cho việc ước lượng đường biên hiệu quả. Thêm nữa, phương pháp phi tham số cũng không bao gồm các giả thiết về phân phối thống kê đối với các sai số. Chính vì vậy, bất kỳ một ngân hàng nào hoạt động ngoài đường biên hiệu quả thì đều coi là phi hiệu quả về mặt kỹ thuật. Ngoài ra, phương pháp này cũng được coi là thích hợp với các mẫu nghiên cứu có quy mô nhỏ. Tuy nhiên, một nhược điểm lớn của cách tiếp cận này là không tính đến các sai số có thể có trong dữ liệu nghiên cứu nghĩa là không tính đến sự tác động của các biến ngẫu nhiên đối với hiệu quả kinh doanh của ngân hàng.
4.2. Phương pháp tham số
Phương pháp tham số là phương pháp đánh giá hiệu quả kinh doanh ngân hàng sử dụng một hàm số mô tả mối quan hệ giữa đầu vào và đầu ra trong kinh doanh ngân hàng với những kỹ thuật phân tích thích hợp. Nội dung của phương pháp tham số được mô tả trong các phần tiếp theo sau đây.
4.2.1. Các hàm số mô tả mối quan hệ giữa đầu vào và đầu ra trong kinh doanh ngân hàng
Khi sử dụng phương pháp tham số để đánh giá hiệu quả kinh doanh của ngân hàng, cần phải ước lượng được dạng hàm số mô tả mối quan hệ giữa đầu vào mà ngân hàng sử dụng để tạo ra các đầu ra trong một thời kỳ nhất định. Các dạng hàm số được dùng phổ biến bao gồm hàm sản xuất Cobb-Douglas và hàm loga siêu việt.
(a) Hàm sản xuất Cobb-Douglas
Hàm Cobb-Douglas là hàm sản xuất được sử dụng phổ biến để mô tả mối quan hệ giữa đầu vào và đầu ra trong quá trình sản xuất kinh doanh của một tổ chức bất kì, được đưa ra bởi Cobb và Douglas (1928). Hàm Cobb-Douglas có dạng cơ bản là:
![]()
![]()
Trong đó, K và L là vốn và lao động được xem là các yếu tố đầu vào cơ bản sử dụng để tạo ra lượng đầu ra Q là hằng số còn α và β là các hệ số co giãn của Q theo K và L. Hàm Cobb-Douglas khi được logarit hóa có dạng:
![]()
![]()
Khi áp dụng trong tính toán hiệu quả kinh doanh của ngân hàng, hàm Cobb-Douglas được mô tả đối với hai trường hợp: tính toán hiệu quả kỹ thuật và hiệu quả chi phí.
– Đối với hiệu quả kỹ thuật, hàm sản xuất Cobb-Douglas có dạng:
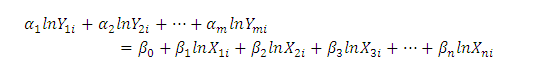
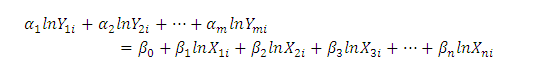
Hàm số này được áp dụng đối với ngân hàng thứ i, sử dụng n đầu ra X để tạo ra m đầu vào Y.
– Đối với hiệu quả chi phí, hàm sản xuất Cobb-Douglas có dạng:
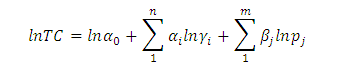
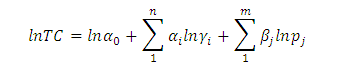
Trong công thức này, TC là tổng chi phí của ngân hàng, γi là đầu ra thứ i còn pj là giá của đầu vào thứ j, α0, αi, βj là những tham số ước lượng được, thể hiện độ co giãn của hàm sản xuất.
(b) Hàm sản xuất Loga siêu việt
Hàm Loga siêu việt giới thiệu bởi Christensen và cộng sự (1973) được coi là một bước phát triển quan trọng kể từ khi hàm Cobb-Douglas được ra đời. Murray & White (1983) là các tác giả lần đầu tiên áp dụng hàm số này để tính toán hiệu quả của ngân hàng và từ đó đến nay, hàm loga siêu việt đã trở thành một công cụ được sử dụng trong các nghiên cứu tiếp theo.
Khi dùng để tính toán hiệu quả kỹ thuật ngân hàng, hàm Loga siêu việt có dạng như sau:
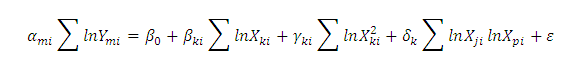
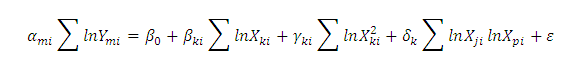
Trong công thức này, ngân hàng thứ i sử dụng N đầu vào để tạo ra M đầu ra với các hệ số co dãn tương ứng.
Khi dùng để tính toán hiệu quả chi phí, hàm Loga siêu việt bổ sung các thông tin về giá cả các đầu vào và có dạng:
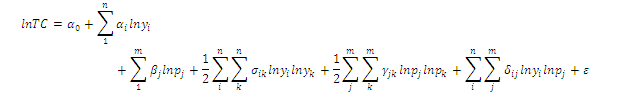
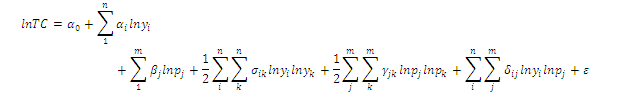
Trong công thức này, TC là tổng chi phí của ngân hàng, γi là đầu ra thứ i còn pj là giá của đầu vào thứ j với sai số thống kê là ε.
4.2.2. Kỹ thuật phân tích đường biên hiệu quả
Các hàm sản xuất mô tả ở phần trên được sử dụng để xây dựng đường biên hiệu quả và được phân tích bằng nhiều kỹ thuật khác nhau. Các kỹ thuật phân tích bao gồm phân tích biên ngẫu nhiên (Stochastic Frontier Analysis -SFA), phương pháp tiếp cận tự do (Distribution Free Approach – DFA) và phương pháp phân tích biên dày (Thick Frontier Analysis – TFA).
(a) Kỹ thuật phân tích biên ngẫu nhiên (SFA)
Kỹ thuật biên phân tích biên ngẫu nhiên được đề xuất bởi Aigner và cộng sự (1977), Battese và Corra (1977), Meeusen và van Den Broeck (1977), dựa trên quan điểm một tổ chức hoạt động bên ngoài đường biên hiệu quả có thể do các yếu tố mà tổ chức đó không thể kiểm soát được. Chính vì vậy, kỹ thuật SFA cho phép sự có mặt của các sai số trong các hàm sản xuất khi xây dựng đường biên hiệu quả. Sai số này được chia thành hai phần, một phần mô tả nhiễu thống kê tuân theo một phân phối mang tính chất đối xứng, phần còn lại gọi là sai số phi hiệu quả, tuân theo phân phối không mang tính chất đối xứng.
Minh họa cho kỹ thuật phân tích này, sử dụng hàm sản xuất có dạng:


(b) Phương pháp tiếp cận tự do (Distribution Free Approach – DFA)
Phương pháp tiếp cận tự do DFA được đưa ra lần đầu tiên bởi Schmidt và Sickles (1984); Berger (1993) trong đó không sử dụng bất kỳ giả thiết nào liên quan đến đặc điểm phân phối của sai số thống kê. DFA cũng sử dụng một dạng hàm cụ thể cho đường biên hiệu quả giống như SFA nhưng lại dùng phương pháp khác để xác định yếu tố phi hiệu quả ra khỏi sai số này. Phương pháp ước lượng các yếu tố phi hiệu quả được dựa trên một giả thiết là các yếu tố phi hiệu quả này tồn tại tương đối ổn định trong suốt khoảng thời gian nghiên cứu trong khi nhiễu ngẫu nhiên sẽ bị triệt tiêu theo thời gian.
Chính vì vậy, một hàm sản xuất sẽ được ước lượng trong từng giai đoạn ngay cả đối với nghiên cứu sử dụng dữ liệu mảng cho nhiều giai đoạn khác nhau bằng các kỹ thuật hồi quy. Phần dư được ước lượng trong mỗi giai đoạn bao gồm yếu tố phi hiệu quả và sai số ngẫu nhiên. Bởi vì sai số ngẫu nhiên của ngân hàng được coi là bị triệt tiêu theo thời gian nên phần dư trung bình ước lượng được trong tất cả các giai đoạn nghiên cứu trở thành yếu tố phi hiệu quả kinh doanh của ngân hàng, và được xác định bằng công thức:


Phương pháp DFA được đánh giá là phương pháp dễ áp dụng hơn SFA do phương pháp này không đòi hỏi những giả thiết về phân phối của sai số thống kê, và vì thế, không cần sử dụng phương pháp hợp lý cực đại (Maximum likelihood methods để ước lượng hàm sản xuất). Thay vào đó, có thể sử dụng nhiều phương pháp ước lượng, chẳng hạn phương pháp bình phương nhỏ nhất tổng quát (GLS) như trong nghiên cứu của Schmidt và Sickles (1984) và phương pháp bình quân nhỏ nhất (OLS) như trong nghiên cứu của Berger (1993).
Bên cạnh ưu điểm kể trên, DFA có nhược điểm là kết quả tính toán hiệu quả có thể khó chính xác nếu như thời gian nghiên cứu quá dài. Ngoài ra, giả thiết các yếu tố phi hiệu quả là không đổi theo thời gian và sẽ bị vi phạm nếu thời gian chưa đủ để có thể triệt tiêu sai số thống kê. Như vậy, tính chính xác của hiệu quả đo lường được sẽ phụ thuộc vào số năm nghiên cứu. De Young (1997b) cho rằng nếu sử dụng 6 năm nghiên cứu thì mô hình này trở nên hợp lý hơn.
(c) Phương pháp phân tích biên dày (Thick Frontier Analysis – TFA).
Phương pháp phân tích biên dày TFA được đưa ra bởi Berger and Humphrey (1991, 1992) cũng xác định dạng hàm sản xuất để xây dựng đường biên hiệu quả như các phương pháp tham số khác. Tuy nhiên, phương pháp này ước lượng đường biên dày hơn để tính toán hiệu quả của các tổ chức trong mẫu nghiên cứu.
Khi sử dụng để tính hiệu quả chi phí, trước hết, phương pháp này ước lượng hàm chi phí cho 25% ngân hàng sử dụng chi phí thấp hơn mức trung bình và 25% ngân hàng sử dụng chi phí nhiều hơn mức trung bình. Những ngân hàng có chi phí thấp này được coi có mức hiệu quả cao hơn trung bình và được sử dụng để xác định đường biên hiệu quả dày. Tương tự, ngân hàng có chi phí cao hơn mức trung bình được coi có hiệu quả thấp hơn mức trung bình. Hai nhóm ngân hàng này được sử dụng để xây dựng hai đường biên khác nhau và khoảng cách giữa hai đường biên đó chính là sự phi hiệu quả của ngân hàng trong khi các sai số trong mỗi đường biên được bắt nguồn từ các yếu tố khác quan như may mắn và nhiễu ngẫu nhiên.
Xuất phát từ việc tính toán khoảng cách chênh lệch giữa hai nhóm ngân hàng có hiệu quả cao và thấp, phương pháp phân tích biên dày TFA không thể tiến hành xác định hiệu quả kinh doanh cho từng ngân hàng cụ thể mà chỉ có thể ước lượng hiệu quả toàn bộ của mẫu. Chính vì vậy, tính chính xác của hiệu quả trong phương pháp này không đáng tin cậy nếu như các giả thiết không được bảo đảm. Tuy nhiên, phương pháp phân tích biên dày TFA cũng có nhiều giá trị khi nhà nghiên cứu chỉ muốn xem xét độ lớn của sự phi hiệu quả kinh doanh của ngân hàng (Berger và Humphrey, 1991).
Tài liệu tham khảo
- Nguyễn Thu Nga (2017). Phân tích mối quan hệ giữa rủi ro tín dụng với hiệu quả kinh doanh của các NHTMCP Việt Nam. Luận án tiến sĩ kinh tế. Trường Đại học Kinh tế Quốc dân.
- Farrell, M.J. (1957), ‘The measurement of productive efficiency’, Journal of the Royal Statistical Society, 120, pp.253-281.
- Koopmans, T. C. (1951), ‘An analysis of production as an efficient combination of activities’, in Koopmans, T. C. (Ed.): Activity Analysis of Production and Allocation, Proceeding of a Conference, pp.33-97, John Wiley and Sons Inc., London.
- Fare, R., Grosskopf, S. and Lovell, C. A. K. (1985), The Measurement of Efficiency of Production, KluwerNijhoff, Boston.
- Berger, A.N. and Mester L.J.(1997), ‘Inside the Black Box: What Explains Differences in the Efficiencies of Financial Institutions?, Journal of Banking and Finance, 21: 895-947.
- Coelli, T.J., Rao, P., O’Donnell, C.J, Battese, G.E.( 2008). “An Introduction to Efficiency and Productivity Analysis.” Springer Science-i-Business Media.2nd Edition.
- Coelli, T. (1996), “A guide to DEAP version 2.1: a data envelopment analysis (computer) program”, CEPA Working Paper 1996/08,. URL: https://www.owlnet.rice.edu/~econ380/DEAP.PDF
- Fadzlan Sufian (2011) “Benchmarking the efficiency of the Korean banking sector: a DEA approach”, Benchmarking: An International Journal, Vol. 18 Issue:1, pp.107-127, https://doi.org/10.1108/14635771111109841
- Benston, G.J. (1965), ‘Branch banking and economies of scale’, Journal of Finance, 20(2), pp. 312-331.
- Berger, A., & Humphrey, D. (1997), ‘Efficiency of Financial Institutions: International Surveyand Directions for Future Research’, European Journal of Operational Research, 98, pp. 175-212.
- Sealey, Calvin W, and James T Lindley (1977), “Inputs, Outputs, and a Theory of Production and Cost at Depository Financial Institutions”, Journal of Finance, 1977, vol. 32, issue 4, pp. 1251-66.
- Drake, L., & Hall, M.J.B., Simper, R. (2006), ‘The impact of macroeconomic and regulatory factors on bank efficiency: anon-parametric analysis of Hong Kong’s banking system’, Journal of Banking and Finance, 30, pp. 1443–1466.
- Charnes, A., Cooper, W. and Rhodes, E. (1978), ‘Measuring efficiency of decision making units’, European journal of operations research, 6(3), pp. 429-444.
- Banker, R. D., Charnes, A., and Cooper, W, W (1984). “Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis”. Management Science, 30(9), pp. 1079-1092.
- Christensen, L.R., Jorgenson, D.W. & Lau, L.J. (1973), “Transcendental Logarithmic Production Frontiers”, The review of economics and statistics, vol. 55, no. 1, pp. 28-45.
- Murray, J.D. & White, R.W (1983), “Economies of Scale and Economies of Scope in Multiproduct Financial Institutions: A Study of British Columbia Credit Unions”, Journal of Finance, vol. 38, no. 3, pp. 887-902.
- Aigner, D.J., Lovell, C.A.K., and Schmidt, P. (1977),‘Formulation and Estimation of Stochastic Frontier Production Function Models’, Journal of Econometrics, 6, pp. 21-37.
- Battese, G.E. and G.S. Corra. (1977), ‘Estimation of a Production Frontier Model with Application to the Pastoral Zone of Eastern Australia’, Australian Journal of Agricultural Economics, 21, pp. 169-179.
- Meeusen, W. & van Den Broeck, J. (1977), ‘Efficiency Estimation from Cobb-DouglasProduction Functions with Composed Error’, International Economic Review, vol.18, no. 2, pp. 435-444.
- Schmidt, P. & Sickles, R.C., (1984), ‘Production Frontiers and Panel Data’, Journal of Business & Economic Statistics, vol. 2, no. 4, pp. 367-374.
- Berger AN, D Hancock and DB Humphrey (1993). “Bank Efficiency Derived from the Profit Function.” J Banking and Finance, 17, pp. 317-347.
- Berger, A.N. & Humphrey, D.B. (1991), “The Dominance of Inefficiencies over Scale and Product Mix Economies in Banking”, Journal of Monetary Economics, vol. 28, no. 1, pp. 117-148.
- 23. Berger, A.N. & Humphrey, D.B. (1992), “Measurement and Efficiency Issues in Commercial Banking” in Output Measurement in the Service Sectors, ed. Z. Griliches, University of Chicago Press, Chicago and London, pp. 245-279.





